|
Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | Next >> Geodesic Dome Notes & Calculatorwritten by Rene K. Mueller, Copyright (c) 2005, 2006, 2007, last updated Tue, January 29, 2019 IntroductionIf you don't care about the origin, the notion, the mathematics behind the geodesic domes, skip right to the 3rd page. Origin of the Geodesic Dome
 's often used notion, but as pointed out before, Walther Bauersfeld created a "geodesic" dome in 1922 for Carl Zeiss in Jena (Germany), he even patented it in Germany 1925 (Patent Nr. 415395) as
seen in this page , so well over 20 years before B. Fuller was developing the "geodesic" approach.
The term "geodesic" is a mathematical term, which was adapted by Fuller to describe his approach, the term otherwise literally means "shortest path of two points on a sphere or curved space".
It seems Fuller simply wasn't aware of Bauersfeld prior work at Carl Zeiss, and reinvented and popularized it then in his life (1895 - 1983) and beyond via the Buckminster Fuller Institute
web-site by Tara Landry and her dome calculator.
The first version of my notes used the strut or chord factors she extracted from books by Hugh Kenner (Geodesic Math & How To Use It) and Lloyd Khan (Domebook I & II), who themselves relied on Fuller's work.
As a result of my study on geodesic polyhedra I wrote my own software tools to calculate, adjust and render 3D solids, such as platonic, archimedean and johnson solids, also generally known as regular and semi-regular polyhedra.
Based on that study of the manifold solids and their geodesic derivates I rewrote my "Geodesic Domes Notes" entirely with more variants (not just Icosahedron based domes) including dedicated calculators for each variant, optimization of cutting respective struts and a 2D construction map.
And as the time goes by I will add more comments on each featured dome variant.
Geodesize: Triangulate & Normalize
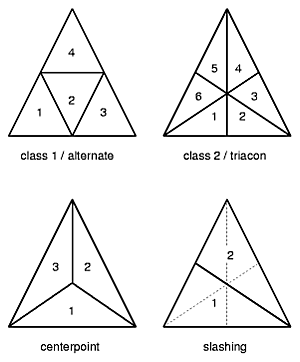
To triangulate a triangle there are different methods or classes available, most prominent are the class 1 or alternate, and class 2 or triacon; additionally several "methods" are distincted - read for more at the References, in particular Joseph D. Clinton's work for NASA.
Of course you can also subdivide into other than triangles, such as other polygonal forms. I focus as a first step on the triangulation and its "class 1" or "alternate" way.
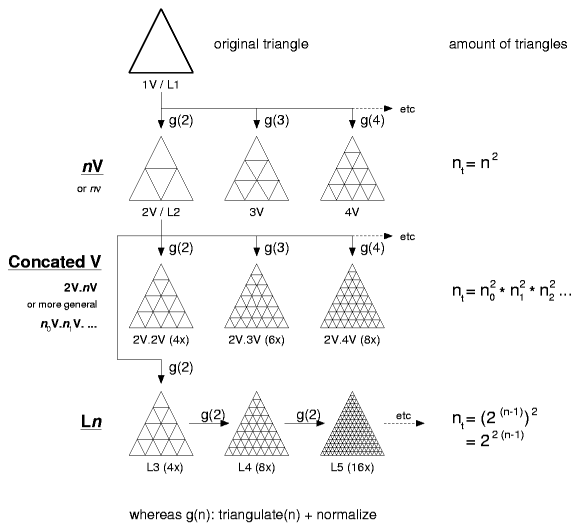
Procedure & Evolution of a Subdividing TriangleI have summarized several procedures incl. ones I discovered (some may have been used by others previously, I'm personally just not aware of it):
The nV NotionBuckminster Fuller introduced the notion of nν often also written as nV (V like in "vision", whereas ν is the greek letter "nu"), it means the amount of division of an original triangle. In this case the class 1 or alternate method is used, and from the original triangle.Formulas: nt = n2 Example: 5V or 5ν has 52 triangles per original triangle The Ln NotionMore in an accident I "geodesized" an already geodesized solid, because the program I wrote could not make subdivisions other than 2 at first, so in order to create 4V I thought to pipe it into the same program twice - and as a surprise the strut lengths varied from the 4V notion - I also came up with 5 strut lengths and not 6 as common for the 4V.I realized then, the triangles were more even, smaller variance of strut lengths. In order to distinct this method from the nV notion I called it Level 1 or L1 and then L2. In order to make it more aligned with the nV notion: 1V and L1 are the same, 2V and L2 are also the same, but 4V and L3 differ then. Formulas: nt = (2(n-1))2 = 22(n-1) Example: L5 = (25-1)2 = 22(5-1) = 256 triangles per triangle The Concated V NotionWhile I discovered a geodesized geodesize solid (like L3) provides different strut lengths and variance than a comperable, in sense of amount of subdivisions nV variant, I extended that it wouldn't necessary be the 2V to derive others, so I introduce the n0V.n1V . . . notion, concate the procedure of geodesize with '.' together.
Formulas: nt = n02 * n12 * n22 ... Example: 2V.3V.2V ~ 12V = 22 * 32 * 22 = 144 triangles per original triangle The Concated V vs Ln Notion
NormalizingIn order to normalize, we need to determine the distance of each vertice (x,y,z) from the center or an origin (xorigin,yorigin,zorigin): d = √(x2 + y2 + z2) or more general d = √((x - xorigin)2 + (y - yorigin)2 + (z - zorigin)2) To normalize we divide each of x, y and z by the distance: x = x / d or more general x = (x - xorigin) / d + xorigin which adjusts the point to have distance of 1 to the center - a sphere is a form where all points of the surface have the same distance to its center; so by normalizing the point is spherized or spherical projected. There is far more math to cover in geodesic approaches, but for now I leave it at this and may extend it later more. A bit more math comes when calculating details of the required struts to compose a dome, this follows on the next page then. References
The next pages go into the details of the geodesic domes variants. Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | Next >> Content:
|
| Home | · | About | · |  Tipi | · |  Yurt | · |  Dome | · | Features | · | Gallery |
Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller
Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm
Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source