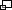Home   ·   About   ·   Tipi   ·   Yurt / Ger   ·   Dome   ·   Features   ·   Gallery About Overview License Tipi Overview Tipi Diary Yurt / Ger Overview Yurt Notes & Calculator Yurt / Ger Diary Yurt Builder Conference Living Notes Material Notes Dome Overview Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Features Overview Chris Aeppli Claudius Kern René K. Müller Geodesic Solitude Johnny's Capsule Geodesic Clay Mud Dome Jurtendorf (Switzerland) Neolithics of Pfyn Strawbale Cabin Dome Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Introduction Mathematics Vertical Stretching Examples Real Life Applications Pro & Contra PVC Zome Links Low Cost Dome (PVC) Miscellaneous Domes Site Search Enter term & press ENTER If you found the information useful, consider to make a donation:   Helix Zome Updates Wed, May 30, 2012: Added photos of a PVC Zome . Tue, December 1, 2009: More description and illustrations, ready to be published . Tue, November 17, 2009: First version with a brief description and mathematical description, and real life applications. . also known as Spinning Circles Zome, Feminin Helix Zome or simply Feminin Zome. 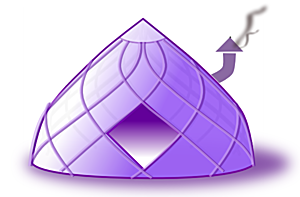Introduction Helix Zome (side view) Helix Zome habitat application The Helix Zome is a variant of a zome composed by half helixes (helix = spiral with a constant diameter). The term "Zome " comes from "zonohedron " + "dome" combined - in strict mathematical terms the Helix Zome isn't a zonohedron anymore, yet, zome is often used for unusual dome variants, so I stick with the term as well. The Helix Zome was developed by Nicolas Causse back in 2006. I met Nicolas personally in summer 2009 and he introduced me to his concept of the Helix Zome. 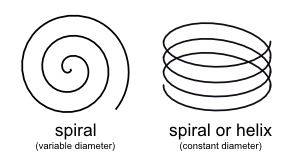Flower of Life Helix Zome (n = 6, top view) From a top view of the Helix Zome reveals circles crossing one central point, circles positioned around a circle, when choosing 6 circles (or helixes) following pattern appears (see left-hand side picture), also known as "Seed of Life", as part of the "Flower of Life". The "Flower of Life " is a metaphysical term, which relates to the origin of life itself, the circle, the first atom, the first entity or singularity, and its surrounding emanations - how circles can be arranged orderly around a central circle - an archetype of form itself. Helix vs Spiral Nicolas insist of the term helix - and not spiral: the term spiral is often used to describe a circular form with an increasing or decreasing diameter, but also includes a constant diameter. At the first sight it may look like a spiral with an increasing or decreasing diameter, but it's a spiral of a constant diameter, for that reason Nicolas calls it a Helix Zome, a helix is a spiral with a constant diameter. Polyhedral (Masculin or Crystal) vs Helical (Feminin or Fluid) Polyhedral Zome Helix Zome The Helix Zome has its origin in its polyhedral form, and Nicolas refined and smoothed it until he found the helix based form, he calls this variant the "feminine" zome, whereas the polyhedral the "masculin" zome. The Helix Zome, from a polyhedral point of view, "represents a sort of combination of infinite frequency along with a finite subdivision", as Rob Bell writes to me; or "infinite frequency (n -> infinite) the polar zonohedron of order n approaches a solid of revolution created by rotation of a sine curve" (source: Chilton and Coxeter 1963, Towle 1996). Mathematics There are several ways to describe the helix zome, let's feature here two of them: Spinning Circles, and Parametric Approach. Spinning 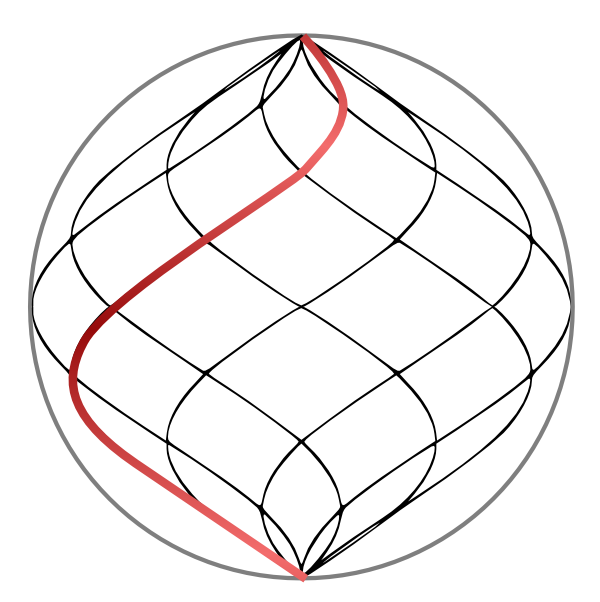Circles side view top view 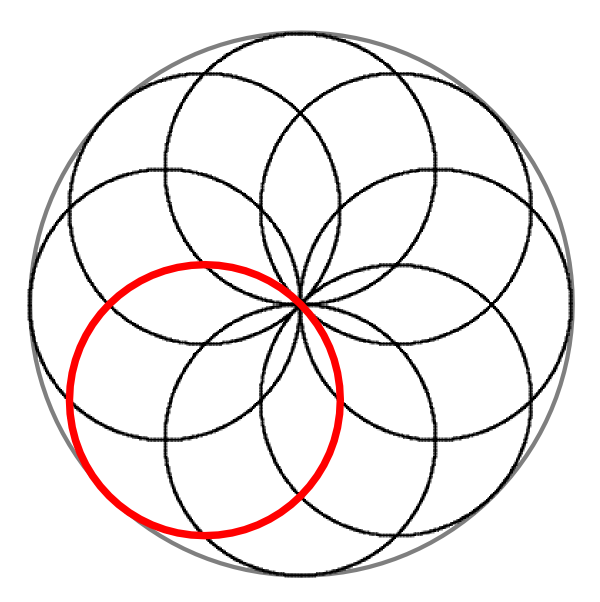Since we cut the form into a helix dome or zome, only half of the spinning is done. Parametric Approach A helix zome is composed by n-amounts of double helix, the coordinate of one partial helix: x = sin(α + β) d/4 + sin(β) d/4 y = cos(α + β) d/4 + cos(β) d/4 z = (α / π) d/2 vs or α / π h whereas α = 0..π, β = (2π / n) i n = amount of double helixes, i = 0..n-1 and d = diameter of the helix zome vs = 1.0 .. 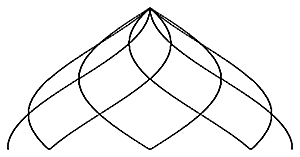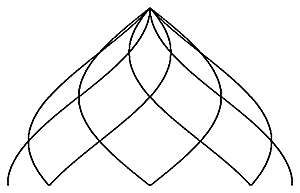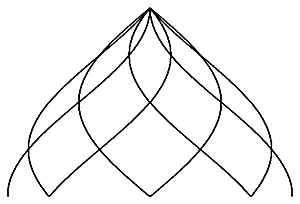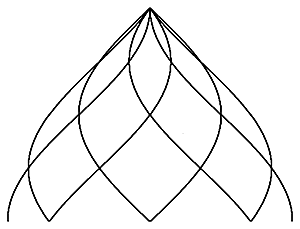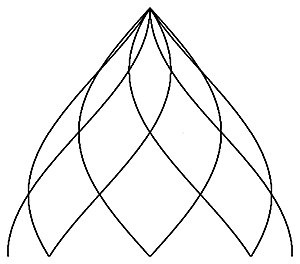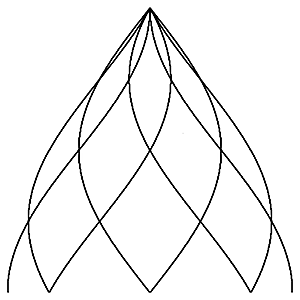2.0 stretch vertically h = height The length of a rib is: lrib = √ ( d2 π2 / 16 + h2 ) considering lrib = √ ((drib π / 2)2 + h2) whereas drib = d / 2 Vertical Stretching For better usage, the helix zome can be vertically stretched, 125% to 150% are suitable for a dome application: 100% 2009/11/30 14:01 125% 2009/11/30 14:01 133% 2009/11/30 14:01 150% 2009/11/30 14:01 175% 2009/11/30 14:01 200% 2009/11/30 14:01 Examples All examples have h = 133% 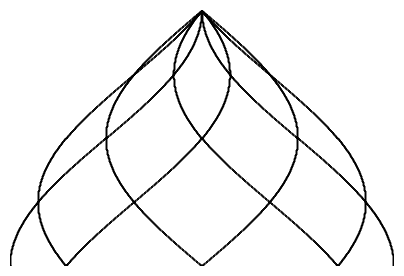side view 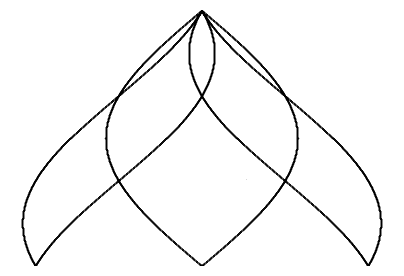n = 6 top view 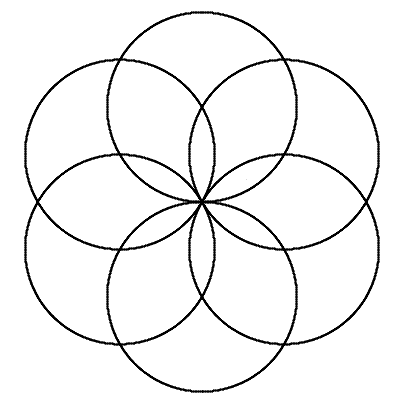n = 6 n = 8 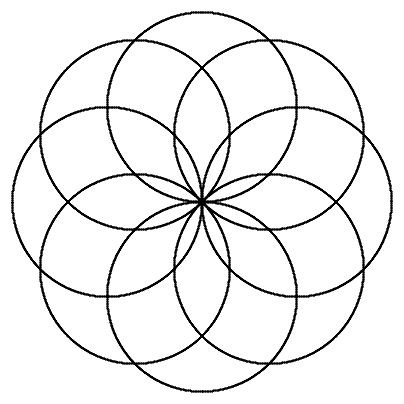n = 8 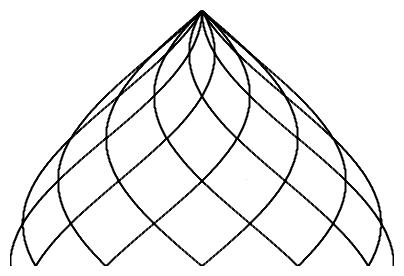n = 12 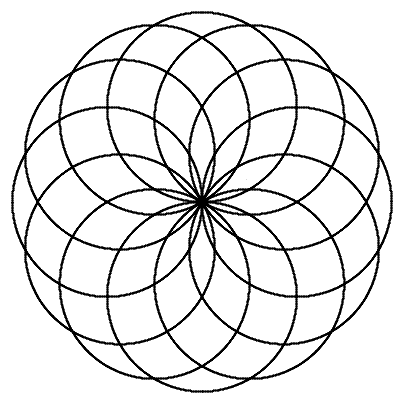n = 12 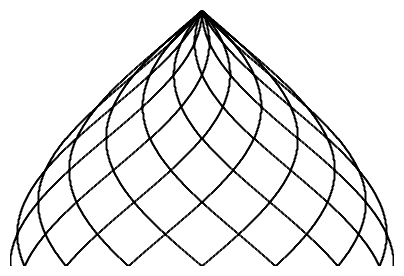n = 16 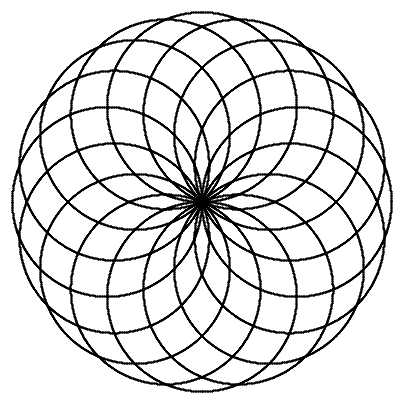n = 16 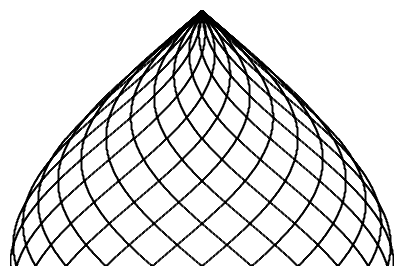n = 24 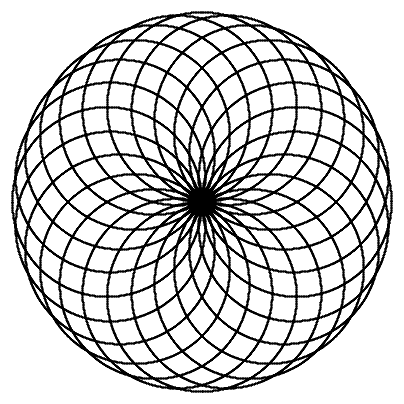n = 24 Real Life Applications Nicolas Causse made a few helix zomes with wood and with interior covers: 2009/12/01 14:30 2009/12/01 14:30 2009/12/01 14:49 2009/12/01 14:49 2009/12/01 14:31 2009/12/01 14:31 2009/12/01 14:31 2009/12/01 14:32 2009/12/01 14:32 2009/12/01 14:32 2009/12/01 14:33 2009/12/01 14:33 Pro & Contra Rib Crossing/Junction Close Up The Helix Zome looks very complex but actually is just composed by helixes but those aren't trivially to be fabricated when you choose a square profile as Nicolas fabricates his helix zomes. He works about 120 hours on a wooden 3m Helix Zome with 10 helixes, with a sophisticated tool to bend 4 smaller ribs into a larger rib. The reason for this overhead is, that the square profile rib is not only spiraled in a constant diameter, but has a slight twist around itself as well so the intersection can be interlocked and the surface remains seamless. I may do some tests with circular profile ribs, either a bent bamboo or a metal torus cut apart. Also, the Helix Zome isn't particular strong in its geometry (top down weakness), and therefore doesn't really suit a larger application unless you triangulate the structure properly. On the other hand it's one of the most beautiful dome applications I came across. PVC Zome Dustin Hoffman used PVC pipes, a simple implementation method: He shared also some of his experiences: What I really learned through the process though was that using 4-way connectors like these was the way to go. Because the more connections you can make at the top within the same vertical space, the better the structure looks. I initially used 8 of these 45 degree connectors which made the top of the zome look all tangled. I wish I could find a 16-way pvc connector, that would be wonderful. The first two photos are from a version woven 3 times. Each pipe crossing 3 other pipes before meeting at the vertex. The other photos are from another take only woven 2 times. Overall this version is much much easier to weave, and provides more headspace because there is less lateral weaving, and each pipe's length is converted into vertical space instead. There is much less tension in the one woven twice, so I was able to make a door with two of the pipes. The pipes are all stuck on rebar stakes which I plant using a rope to ensure they adhere to a perfect circle. Links Heliss.com , the primary source of the Helix Zome .:. Home   ·   About   ·   Tipi   ·   Yurt   ·   Dome   ·   Features   ·   Gallery Print   ·   Bookmark Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source