|
Triangulated Bow Domewritten by Rene K. Mueller, Copyright (c) 2007, last updated Sat, October 6, 2007
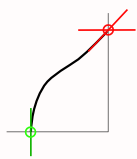
IntroductionAfter I studied the Geodesic Dome I thought about triangulating also other non-(hemi)spherical forms, e.g. a general Bow Dome as I covered already using Bezier curve to simulate bending of bows. One of the disadvantages of the dome is that the roof has too litte steep slope in order to have snow slide down, so it would be interesting to have a circular bow dome with a minimum of slope, like a Yurt, yet, triangulated.
Please Note: This is a very preliminary version of the document, and may change dramatically (e.g. such as used notions) or be renamed. In particular I like to optimize the amount of different struts for each version, and later also add an online calculator for each featured option.
Regular Dome
Steep Roof Dome
Dent Roof Dome
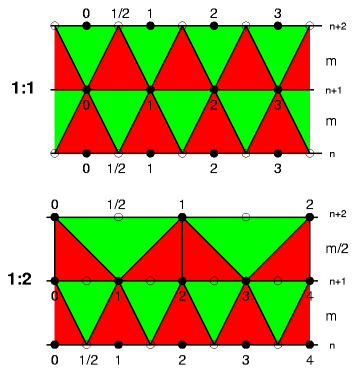
It needs to be said in case of dome, no matter what variant, that the entire surface acts as roof, in other words, all cover requires 100% sealed of rain water. Stripe TriangulationThe Bezier curve is linearly split into n/2-steps, where n*2 amount of edges of the polygon for the base, that outline is rotated to create a circular space, and triangulated in stripes. Methods of Stripe TriangulationThere are two ways to stripe triangulate as I focus on (there are many other methods available), keeping the amount of edges constant, or reduce them by half when a certain length is reached:
The detail about switching to from 1:1 triangulation to 1:2 when a certain minimum length is reached (aka as "trimming"):
References
OverviewHere an overview of a couple of options, for now I feature only Method B ("trimmed lamella") with 1:2 triangles when it narrows:
Triangulated Bow Dome 0° / 0°
Triangulated Bow Dome 25° / 0°
Triangulated Bow Dome 45° / 0°
Content:
|
| Home | · | About | · |  Tipi | · |  Yurt | · |  Dome | · | Features | · | Gallery |

Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller
Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm
Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source